Answer:
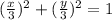
or x² +y²= 9
Explanation:
In Cartesian form, the equation is expressed only in terms of y and x.
x= -3sin(t) -----(1)
y= 3cos(t) -----(2)
I've written x instead of x(t) as in the later part of the working, we will be having an equation of only x and y, thus x will no longer be a function of t. This applies to equation 2, where I have replaced y(t) with y.
Relating sine to cosine:
sin²(t) +cos²(t)= 1
[sin(t)]² +[cos(t)]²= 1 -----(3)
From (1):
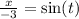
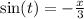 -----(3)
-----(3)
From (2):
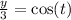
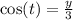 -----(4)
-----(4)
Substitute (4) &(5) into (3):
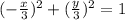
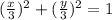
The steps below are optional as the above is already considered to be the Cartesian form.
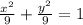
Multiplying both sides by 9:
x² +y²= 9