Question

Listed below are the amounts of net worth (in millions of dollars of the ten wealthiest celebrities in a country. Construct a 95% confidence interval. What does the result tell us about the population of all celebrities? Do the data appear to be from a normally distributed population as required? 155 153 147 147 147 147 260 206 199 156 What is the confidence interval estimate of the population mean μ? S□ million su«s□ million (Round to one decimal place as needed.)

Answer 1

95% of confidence interval are (144.74 , 199.23)

Explanation:

given data 155 153 147 147 147 147 260 206 199 156

given sample n =10

`mean = ∑x / n = (155+ 153+ 147 +147+ 147= 147= 260+ 206 +199+ 156 )/(10)`

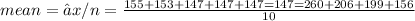
mean = 171.7≅ 172

x x- mean (x-mean)^2

155 155-172= -17 289

153 153-172 = -19 361

147 147-172 = -25 625

147 147-172 = -25 625

147 147-172 = -25 625

147 147-172 = -25 625

260 260-172 = 88 7784

206 206-172 = 34 1156

199 199-172 = 27 729

156 156-172 = -16 256

∑ (x-mean)^2 = 13,075

Sample variance S^2 = ∑ (x-mean)^2 / n-1 = 13,075 / 10-1 =1452.77

sample standard deviation S = √variance = 38.11

95% confidence interval

The degrees of freedom = n-1 = 10-1 =9

The tabulated value 't' = 2.26 at '9' degrees of freedom at 95% level of significance

χ ± 2.26 S / √n

172 ± 2.26 (38.11)/√10

The intervals are (172 - 2.26 (38.11)/√10 , 172 + 2.26 (38.11)/√10)

( 172 - 27.236 , 172+27.236)

(144.74 , 199.23)

there fore the 95% of confidence interval are (144.74 , 199.23)