Question

A mass of 4 kg is initially moving in the +x direction and collides inelastically with a mass of 8 kg moving in the -x direction at 7 m/s. After the collision, both masses move in the +x direction at 4 m/s. How fast was the 4 kg moving before the collision in m/s?

Answer 1

The initial velocity of 4 kg mass in positive 'x' direction is 26 m/s.

Step-by-step explanation:

Consider the positive direction to have positive value and negative direction to have negative value.

Let the initial velocity of 4 kg mass be 'u' m/s in the positive 'x' direction.

Given:

Mass of body moving in positive direction is,
`m_1=4\ kg`

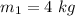
Mass of body moving in negative direction is,
`m_2=8\ kg`

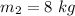
Initial velocity of 8 kg mass is,
`u_2=-7\ m/s`

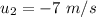
Combined velocity of the masses after collision is,
`v=4\ m/s`

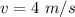
We know that, for an inelastic collision, the total momentum is conserved before and after collision. So,

Initial momentum of the masses = Final momentum of the masses

`m_1u_1+m_2u_2=(m_1+m_2)v\\\\\textrm{Expressing in terms of }u_1,\textrm{we get:}\\\\m_1u_1=(m_1+m_2)v-m_2u_2\\\\u_1=((m_1+m_2)v-m_2u_2)/(m_1)`

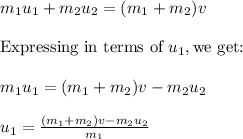
Now, plug in the given values and solve for 'u₁'. This gives,

`u_1=((4+8)4-[8*(-7)] )/(4)\\\\u_1=(12* 4-(-56))/(4)\\\\u_1=(48+56)/(4)\\\\u_1=(104)/(4)\\\\u_1=26\ m/s`

Therefore, the initial velocity of 4 kg mass in positive x direction is 26 m/s.