Question

BIO Human Energy vs. Insect Energy.

For its size, the common flea is one of the most accomplished jumpers in the animal world. A 2.0-mm-long, 0.50-mg flea can reach a height of 20 cm in a single leap. Ignoring air drag, what is the takeoff speed of such a flea?

Answer 1

To find the takeoff speed of a flea, we use Newton's second law of motion and the given forces and mass of the flea. The acceleration of the flea can be calculated using the sum of the forces and the mass, and then the takeoff speed can be found using the acceleration and the height of the jump.

Step-by-step explanation:

To find the takeoff speed of a flea, we need to use Newton's second law of motion, which states that force is equal to mass times acceleration. In this case, the force exerted by the flea is the sum of the force exerted by the flea on the ground and the force exerted by the breeze blowing on the flea. We can calculate the acceleration of the flea using the equation:

F_total = mass * acceleration

where F_total is the sum of the forces exerted on the flea, and mass is the mass of the flea. Rearranging the equation to solve for acceleration, we get:

acceleration = F_total / mass

Plugging in the values for force and mass given in the question, we can calculate the acceleration of the flea. Once we have the acceleration, we can use it to find the takeoff speed of the flea using the equation:

takeoff speed = sqrt(2 * acceleration * height)

Answer 2

The takeoff speed of the flea is 1.98 m/s.

Step-by-step explanation:

Consider upward direction as positive and downward direction as negative.

Given:

Length of the flea (L) = 2.0 mm

Mass of the flea (m) = 0.50 mg

Maximum height reached by the flea (h) = 20 cm = 0.20 m [1 cm =0.10 m]

At maximum height, velocity is 0. So, final velocity (v) = 0 m/s

Acceleration of the flea is only due to gravity (g) = -9.8 m/s² (Down)

Let the initial takeoff velocity be 'u' m/s.

We know that, from kinetic equation of motion, the final velocity is related to initial velocity, acceleration and displacement as:

`v^2=u^2+2aS`

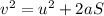
Where, 'a' and 'S' are the acceleration and displacement of the body respectively.

As per question,

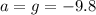`a = g = -9.8` m/s²

`S = h = 0.20\ m`

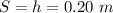
Plug in the given values and solve for 'u'. This gives,

`0=u^2-2* 9.8* 0.20\\\\u^2=3.92\\\\√(u^2)=√(3.92)\\\\u=1.98\ m/s`

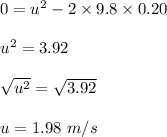
Therefore, the takeoff speed of the flea is 1.98 m/s.