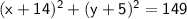Question

Write the standard equation of the circle with the center ​(-14​,-5​) that passes through the point ​(​-7,​5).

Answer 1

`\sf (x+14)^2+(y+5)^2=149`

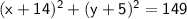
Explanation:

Standard equation of a circle:
`\sf (x-a)^2+(y-b)^2=r^2`

(where (a, b) is the center and r is the radius of the circle)

Substitute the given center (-14, -5) into the equation:

`\sf \implies (x-(-14))^2+(y-(-5))^2=r^2`

`\sf \implies (x+14)^2+(y+5)^2=r^2`

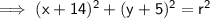
Now substitute the point (-7, 5) into the equation to find r²:

`\sf \implies ((-7)+14)^2+(5+5)^2=r^2`

`\sf \implies (7)^2+(10)^2=r^2`

`\sf \implies 149=r^2`

Final equation:

`\sf (x+14)^2+(y+5)^2=149`

Answer 2

equation: (x + 14)² + (y + 5)² = 149

Given:

• centre : ​(-14​,-5​)

• point ​(​-7,​5)

=============

Formula's:

• (x-h)² + (y-k)² = r²

• centre : (h, k)

• radius : r

• distance between points :
  `\sf √((x2-x1)^2 + (y2-y1)^2)`

Find the radius:

`\rightarrow \sf √((-7-(-14))^2 + (5-(-5))^2)`

`\sf \rightarrow √(\left(-7+14\right)^2+\left(5+5\right)^2)`

`\sf \rightarrow √(149)`

Equation of circle:

• (x-h)² + (y-k)² = r²

• (x-(-14))² + (y-(-5))² = (√149)²

• (x + 14)² + (y + 5)² = 149

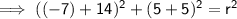
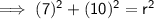
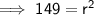
Graph for clarification: