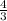Given:
Line
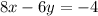
To find:
Slope of the perpendicular line and slope of the parallel line.
Solution:
Equation of a given line:
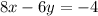
Subtract 8x on both sides, we get
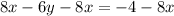
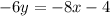
Divide by -6 on both sides.
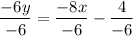
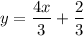
Slope of this line is
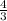 .
.
If two lines are perpendicular then their slopes are negative inverse of one another.
Slope of perpendicular line =
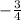
If two lines are parallel, then their slopes are equal.
Slope of perpendicular line =