Question

Train A has a speed 15 miles per hour greater than that of train B. If train A travels 280 miles in the same time train B travels 250 miles, what are the speeds of the two trains?

Answer 1

Explanation:

Let's make a table to keep track of the info.

d = r * t

Train A

Train B

Now we just need to fill it in! Let's look at the rates first, since that's the first bit of info given. Train A is going 15 miles per hour faster than Train B, but because we don't know how fast either is going, we will say that the rate of B is r, and the rate of A then is r + 15. Let's put that in the table.

d = r * t

Train A r + 15

Train B r

The distance Train A travels is 280 and the distance Train B travels is 250:

d = r * t

Train A 280 = r + 15

Train B 250 = r

We're getting there. We just need the time now. We don't have it, but we do know they left at the same time, t, so

d = r * t

Train A 280 = r + 15 * t

Train B 250 = r * t

The distance formula is d = rt, as illustrated in the way the table is set up, so let's get the distance formula for each train.

Train A: 280 = t(r + 15)

Train B: 250 = rt

Can't do much with that right now, but let's think about equality here for a minute. If the time is the same for both trains, then

t for Train A = t for Train B

Let's solve each of those distance equations for t and set them equal to each other:

Train A:

`t=(280)/(r+15)`

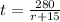
Train B:

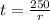`t=(250)/(r)` and setting them equal to each other because t = t:

`(280)/(r+15) =(250)/(r)`

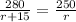
Cross multiply to get

280r = 250r + 3750 and

30r = 3750 so

r = 125

Train B is going 125 mph and Train A is going 140 mph. A bit fast, if I do say so myself.