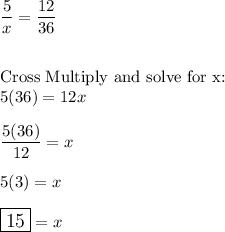Question

an architect wants to build three similar triangles such that the ratio of the middle triangle. The smallest one has side lengths 5, 12, and 13; the largest triangle has the side lengths 45, 108, and 117. If two of the middle triangle's sides are 39 and 36, what is the length of the third side? ​

Answer 1

Answer: 15

Explanation:

small: 5 12 13

middle: __ 36 39

large: 45 108 117

Notice that to get from the small to the large, multiplied by 9

5(9) = 45 12(9) = 108 13(9) = 117

That is because the sides are proportional
`(5)/(45)=(12)/(108)=(13)/(117)\rightarrow(1)/(9)`

To get from small to middle, multiply by 3

5(3) = 15 12(3) = 36 13(3) = 39

To solve it using proportions:

`(5)/(x)=(12)/(36)\\\\\\\text{Cross Multiply and solve for x:}\\5(36)=12x\\\\(5(36))/(12)=x\\\\5(3)=x\\\\\large\boxed{15}=x`