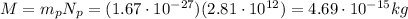a) the number of protons is
 more than the electrons
more than the electrons
b)
Step-by-step explanation:
The net electric charge on the ball is
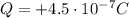
This electric charge is given by the algebraic sum of the charge of the protons and of the charge of the electrons.
The charge of one proton is:
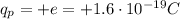
While the charge of one electron is
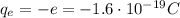
So the net charge on the metal ball will be given by
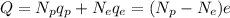
where
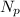 is the number of protons
is the number of protons
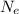 is the number of electrons
is the number of electrons
So we find:
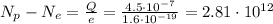
This means that the number of protons is
 more than the electrons.
more than the electrons.
b)
In this case, we want to make the ball neautral, so we have to remove a net charge of Q' such that the new charge is zero:
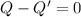
This implies that the charge that we must remove is
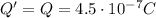
To do that (and to make the ball losing mass at the same time), we have to remove protons, since they have positive charge.
The number of protons that must be removed is:
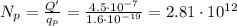
The mass of one proton is
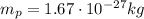
Therefore, the total mass that must be removed from the ball is