Answer:
The largest two consecutive odd integers are
19 and 21
Explanation:
Let
x ----> the first consecutive odd number
x+2 ---> the second consecutive odd number
we know that
The inequality that represent this situation is
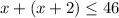
solve for x
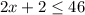
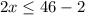
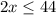

therefore
The largest two consecutive odd integers are
19 and 21