Question

What is the equation process to this question?

Evaluate the function to answer the question.

The height h, in feet, of a ball that is released 4 ft above the ground with an initial upward velocity of 80 ft/s is a function of the time t, in seconds, the ball is in the air and is given by the following.

h(t) = −16t^2 + 80t + 4, 0 ≤ t ≤ 5.04

(a) Find the height of the ball (in feet) above the ground 2 s after its released.

(b) Find the height of the ball (in feet) above the ground 4 s after its released.

Answer 1

The given equation is
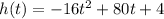`h(t)=-16t^2+80t+4` where h is the height, in feet, of a ball and t is the time, in seconds.

Part a: The height of the ball when t = 2 seconds:

The height of the ball above the ground 2 seconds after it is released can be determined by substituting t= 2 in the equation
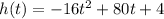`h(t)=-16t^2+80t+4`, we get;

`h(2)=-16(2)^2+80(2)+4`

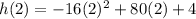
Simplifying the terms, we get;

`h(2)=-64+160+4`

`h(2)=100`

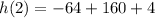
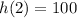
Thus, the height of the ball after 2 seconds is 100 feet.

Part b: The height of the ball when t = 4 seconds:

The height of the ball above the ground 4 seconds after it is released can be determined by substituting t = 4 in the equation
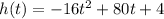`h(t)=-16t^2+80t+4`, we get;

`h(4)=-16(4)^2+80(4)+4`

Simplifying the terms, we get;

`h(4)=-256+320+4`

`h(4)=68`

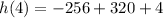
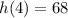
Thus, the height of the ball after 4 seconds is 68 feet.