Question

There is a product that is defective with the probability of 0.03. They are sold in packages of 12. The company offers money back if two or moreare defective. What is the probability that a given package will be returned for cash?

Answer 1

0.04865 or 4.9%

Explanation:

This is a binomial distribution function which is expressed as:

`P(X=x){n\choose x}p^x(1-p)^(n-x)`

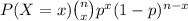
Where:

• p=probability of success
• x=number of successful events
• n=size of the sample

Given that p=0.03, n=12 and x=2+, the probability of a cash back is calculated as:

`P(X=x){n\choose x}p^x(1-p)^(n-x)\\\\P(X\geq 2)=1-P(X\leq 1)\\\\=1-[{12\choose 0}0.03^0(0.97)^(12)+{12\choose 1}0.03^1(0.97)^(11)]\\\\\\=1-[0.69384+0.25751]\\\\\\=0.04865`

Hence, the probability of a cash return is 0.04865 or 4.9%