Question

F(x)=-3(x-2)^2+27
Reveal the y intercept

Answer 1

The y-intercept is: (0, 15)

The graph is also attached below.

Explanation:

Given

`f\left(x\right)=-3\left(x-2\right)^2+27`

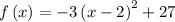
Determining the y-intercept

As we know that y-intercept is the point on a graph where x = 0

so

Putting x = 0 in the function

`y=-3\left(0-2\right)^2+27`

`y=-2^2\cdot \:3+27`

`y=-12+27`

`\mathrm{Add/Subtract\:the\:numbers:}\:-12+27=15`

`y=15`

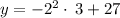
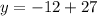
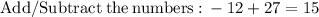
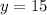
Therefore, the y-intercept is: (0, 15)

The graph is also attached below.