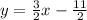Question

Write an equation of the perpendicular bisector of the line segment whose endpoints are (−1,1) and (7,−5)

Answer 1

The equation is
`y = (3)/(2) x - (11)/(2)`

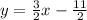
Step-by-step explanation:

We have to first find the mid-point of the segment, the formula for which is

`((x_1+x_2)/(2) , (y_1+y_2)/(2) )`

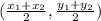
So, the midpoint will be
`((-1+7)/(2) , (1-5)/(2) )\\\\`

=
`(3,-2)`

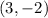
It is the point at which the segment will be bisected.

Since we are finding a perpendicular bisector, we must determine what slope is perpendicular to that of the existing segment. To determine the segment's slope, we use the slope formula
`(y_2-y_1)/(x_2-x_1)`

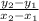
The slope is
`(-5-1)/(7+1)` =
`-(2)/(3)`

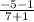Perpendicular lines have opposite and reciprocal slopes. The opposite reciprocal of
`-(2)/(3)` is
`(3)/(2)`

To write an equation, substitute the values in y = mx + c

WHere,

y = -1

x = 3

m = 3/2

Solving for c:

`-1 = (3)/(2) X 3 + c\\\\-1 = (9)/(2)+c\\ \\c = (-2-9)/(2) \\\\c = (-11)/(2)`

Thus, the equation becomes:

`y = (3)/(2) x - (11)/(2)`