Note: Your system of equations is missing some details. Since the procedure is same so it should not be matter as it would still make your understand the concept. So I am assuming you have the following system of equations:
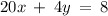

Answer:
The two lines intersect at (3/31, 47/31) which is the solution to this system of equations.
The graph of the solution is also attached below.
Explanation:
Given the system of the equations
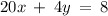

The solution will be the point of intersection of two lines. So we need to solve the system of the equations to find the point of intersection in order to graph the solution.
Solving
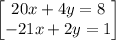
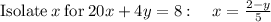
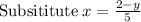
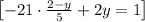


 ∵
∵
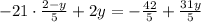
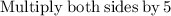
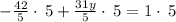
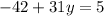
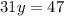
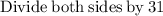
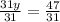

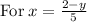
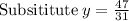
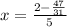
as
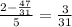
so
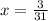
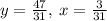
Therefore, the two lines intersect at (3/31, 47/31) which is the solution to this system of equations.
The graph of the solution is also attached below.