Question

Solve using the fundamental theorem of algerba
(x+7)^7

Answer 1

Explanation:

Given

`\left(x+7\right)^7`

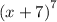
solving the expression

`\left(x+7\right)^7=0`

`\mathrm{Using\:the\:Zero\:Factor\:Principle:\quad \:If}\:ab=0\:\mathrm{then}\:a=0\:\mathrm{or}\:b=0\:\left(\mathrm{or\:both}\:a=0\:\mathrm{and}\:b=0\right)`

`\mathrm{Solve\:}\:x+7=0`

`\mathrm{Subtract\:}7\mathrm{\:from\:both\:sides}`

`x+7-7=0-7`

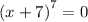
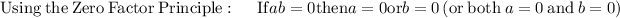
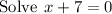
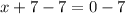
Simplify

`x=-7`

`\mathrm{The\:solution\:is}`

`x=-7`

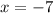
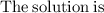
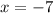
• The fundamental theorem of algebra states that every polynomial function with a degree greater than or equal to 1 has at least 1 complex root.

A complex number follows this form

`a + ib`

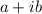
Here:

• The term
  `a` is the real part, and

• The term
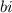  `bi` is the imaginary part.

If b = 0, then the number is a real number.

As -7 has contains only the real part, so the root -7 is the real root.