Question

A pulse moving to the right along the x axis is represented by the function of

wave:

y (x, t) = 2 / (x-3t) ^ 2 + 1

Where x and are measured in centimeters and t in seconds.
a) Find the velocity, pulse amplitude, and expressions for the wave function at t = 0s, t = 1.0s
and t = 2.0 seconds.
b) What would happen if the wave function were:
y (x, t) = 2 / (x + 3t) ^ 2 + 1
How would this change the situation?

Answer 1

(a) Peak=2 cm, velocity= 3 cm/s (to the right)

(b) Peak= 2 cm, velocity= -3 cm/s (to the left)

Step-by-step explanation:

Pulse Movement

The function of a moving wave is given by

`\displaystyle y(x,t)=(2)/((x-3t)^2+1)`

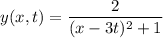
where x,y are measured in cm and t in seconds.

Please check the graph shown in the image provided below. It shows the waveform at two different times, t=0 sec and t=1 sec. The peak value is displaced by 3 cm when t varies by 1 second. It shows a velocity of 3 m/s.

(a) For a given time, say t=0 the expression for the pulse is

`\displaystyle y(x,0)=(2)/(x^2+1)`

The maximum value or the pulse amplitude occurs when the denominator has its minimum value, that is when x=0

`\displaystyle A=y(0,0)=(2)/(0^2+1)=2`

At t=1 second, the function is

`\displaystyle y(x,1)=(2)/((x-3)^2+1)`

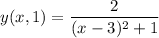
Again, the maximum value of the wave occurs at the minimum value of the denominator, or when

`x-3=0 \rightarrow x=3`

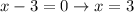
Note the peak has moved 3 cm to the right when t increased by 1 second, this gives us a horizontal velocity of 3 cm/s.

We can corroborate for the general case knowing the peak value moves to the right at the point where

`x-3t=0 \rightarrow x=3t`

Taking the derivative with respect to t gives us the horizontal velocity:

`x'=3\ cm/s`

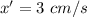
At t=2 seconds

`\displaystyle y(x,2)=(2)/((x-6)^2+1)`

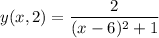
The amplitude and velocity are the same as determined before. The graph shown in the figure attached shows the pulse waves at t=0 and t=1

b) If the function was

`\displaystyle y(x,t)=(2)/((x+3t)^2+1)`

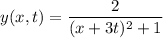
Then when t increases, the peak value moves to the left on the x-axis. The velocity would be

`x'=-3\ cm/s`

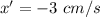
It means the wave is traveling to the left instead of to the right