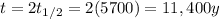A) 320 count/min
B) 40 count/min
C) 80 count/min, 11400 years
Step-by-step explanation:
A)
The activity of a radioactive sample is the number of decays per second in the sample.
The activity of a sample is therefore directly proportional to the number of nuclei in the sample:
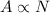
where A is the activity and N the number of nuclei.
As a consequence, since the number of nuclei is proportional to the mass of the sample, the activity is also directly proportional to the mass of the sample:
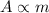
where m is the mass of the sample.
In this problem:
- When the mass is
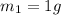 , the activity is
, the activity is

- When the mass is
 , the activity is
, the activity is

So we can find A2 by using the rule of three:
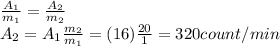
B)
The equation describing the activity of a radioactive sample as a function of time is:
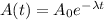 (1)
(1)
where
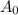 is the initial activity at time t = 0
is the initial activity at time t = 0
t is the time
 is the decay constant, which gives the probability of decay
is the decay constant, which gives the probability of decay
The decay constant can be found using the equation
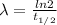
where
 is the half-life, which is the amount of time it takes for the radioactive sample to halve its activity.
is the half-life, which is the amount of time it takes for the radioactive sample to halve its activity.
In this problem, carbon-14 has half-life of

So its decay constant is
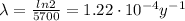
We also know that the tree died
t = 17,100 years ago
and that the initial activity was
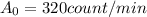 (value calculated in part A, corresponding to a mass of 20 g)
(value calculated in part A, corresponding to a mass of 20 g)
So, substituting into eq(1), we find the new activity:
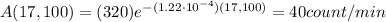
C)
We know that a sample of living wood has an activity of
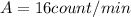 per 1 g of mass.
per 1 g of mass.
Here we have 5 g of mass, therefore the activity of the sample when it was living was:
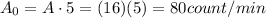
Moreover, here we have a sample of 5 g, with current activity of
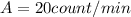 : it means that its activity per gram of mass is
: it means that its activity per gram of mass is
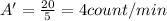
We know that the activity halves after every half-life: Here the activity has became 1/4 of the original value, this means that 2 half-lives have passed, because:
- After 1 half-life, the activity drops from 16 count/min to 8 count/min
- After 2 half-lives, the activity dropd to 4 count/min
So the age of the wood is equal to 2 half-lives, which is: