Answer:
22.4 hours
Explanation:
The population of bacteria is modelled by the equation:
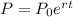
From the the question, the initial population of bacteria is 720.
So after 26 hours, we have:
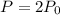
This implies that:
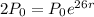
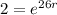
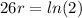
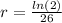
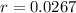
We want to find how long it will take for there to be 1310 bacteria present.
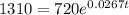
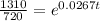
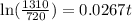
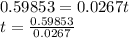
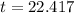
To the nearest tenth , it will take 22.4 hours