Answer:
option A is true.
Explanation:
Given the function
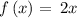
As
The function has no undefined points nor domain constraints. Therefore, the domain is:
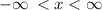
Therefore,
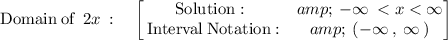
The range of polynomials with odd degree is all the real numbers.
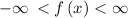
Therefore,

as
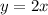
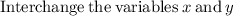
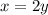
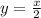
Therefore,
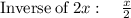
Finding the domain of
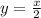 .
.
Again the function
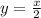 has no undefined points nor domain constraints. Therefore, the domain is:
has no undefined points nor domain constraints. Therefore, the domain is:
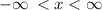
Therefore, the domain of the inverse of f(x) is:
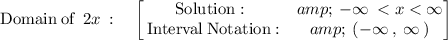
Also the domain of the inverse is the range values of the original function.
Thus, the domain of the inverse of f(x) is the set of any real number, which can also be denoted as:
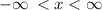
Therefore, option A is true.