Answer:
a) x=-2 or x=-1
b) x=-1.5
c) (-1.5,-0.25)
Explanation:
The given function is
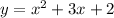
We complete the square as follows:
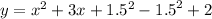
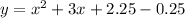
We factor the perfect square;
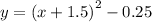
We obtained the vertex form of the function.
a) To find the zeros, we set y=0.
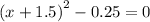
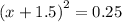

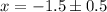
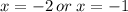
b) The parabola in the form
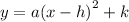
has axis of symmetry at x=h.
Comparing this to
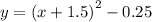
We have

as the axis of symmetry.
The vertex is (h,k)=(-1.5,-0.25)