Answer:
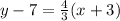
Explanation:
Hi there!
We are given the point (-3, 7)
We want to write the equation of the line containing that point, in point slope-form, and that is also parallel to 4x-3y=7
Parallel lines contain the same slope
So first, let's find the slope of 4x-3y=7
To do that, we can convert the line from standard form (ax+by=c) to slope-intercept form (y=mx+b, where m is the slope, and b is the y intercept)
To do that, we need to isolate y on one side
So start by subtracting 4x from both sides
4x-3y=7
-4x -4x
________________
-3y=-4x+7
Divide both sides by -3
y=
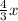 -
-
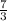
Since 4/3 is in the place of where m should be, the slope of the line is 4/3
It is also the slope of our new line, which we are trying to find
As stated earlier, we want to write this line in point-slope form, which is
 , where m is the slope and
, where m is the slope and
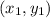 is a point
is a point
This is where the point we were given earlier comes in. We simply need to substitute our values (of the point and the slope) into the formula to find the equation.
First, with the slope; substitute 4/3 as m in the equation
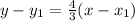
Now substitute -3 as
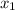 in the equation
in the equation

We can simplify this to:
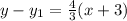
Now substitute 7 as
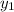 into the equation
into the equation
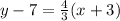
Hope this helps!