Answer: The percent yield of the reaction is 91.8 %
Step-by-step explanation:
To calculate the number of moles, we use the equation:
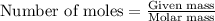 .....(1)
.....(1)
- For
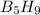 :
:
Given mass of
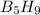 = 4.0 g
= 4.0 g
Molar mass of
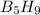 = 63.12 g/mol
= 63.12 g/mol
Putting values in equation 1, we get:
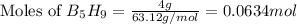
Given mass of oxygen gas = 10.0 g
Molar mass of oxygen gas = 32 g/mol
Putting values in equation 1, we get:
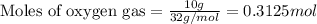
The chemical equation for the reaction of
 and oxygen gas follows:
and oxygen gas follows:

By Stoichiometry of the reaction:
12 moles of oxygen gas reacts with 2 moles of
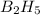
So, 0.3125 moles of oxygen gas will react with =
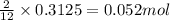 of
of
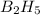
As, given amount of
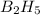 is more than the required amount. So, it is considered as an excess reagent.
is more than the required amount. So, it is considered as an excess reagent.
Thus, oxygen gas is considered as a limiting reagent because it limits the formation of product.
By Stoichiometry of the reaction:
12 moles of oxygen gas produces 5 moles of
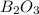
So, 0.3125 moles of oxygen gas will produce =
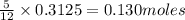 of water
of water
Now, calculating the mass of
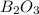 from equation 1, we get:
from equation 1, we get:
Molar mass of
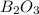 = 69.93 g/mol
= 69.93 g/mol
Moles of
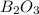 = 0.130 moles
= 0.130 moles
Putting values in equation 1, we get:
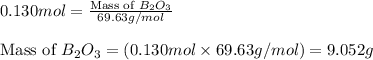
To calculate the percentage yield of
 , we use the equation:
, we use the equation:
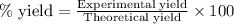
Experimental yield of
 = 8.32 g
= 8.32 g
Theoretical yield of
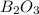 = 9.052 g
= 9.052 g
Putting values in above equation, we get:
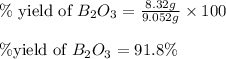
Hence, the percent yield of the reaction is 91.8 %