Answer:
The height of the pole is 105ft,
Explanation:
Let us call
 the height of the pole, then we know that the distance from the bottom of the pole to the anchor point is 49, or it is
the height of the pole, then we know that the distance from the bottom of the pole to the anchor point is 49, or it is
 .
.
The wire length
 is 14 ft longer than height
is 14 ft longer than height
 , hence
, hence
 .
.
Thus we get a right triangle with hypotenuse
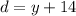 , perpendicular
, perpendicular
 , and base
, and base
 ; therefore, the Pythagorean theorem gives
; therefore, the Pythagorean theorem gives
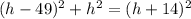
which upon expanding we get:
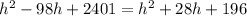
further simplification gives
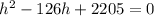 ,
,
which is a quadratic equation with solutions
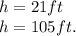
Since the first solution
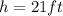 will give the triangle base length of
will give the triangle base length of
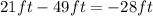 which is negative; therefore, we disregard it and pick the solution
which is negative; therefore, we disregard it and pick the solution
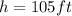 .
.
Hence, the height of the pole is 105ft.