Answer:

Explanation:
In
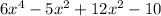 we can rewrite the expression as:
we can rewrite the expression as:
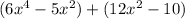 to factor each part individually:
to factor each part individually:
First in
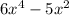 we can factor out the GCF (x²) to find:
we can factor out the GCF (x²) to find:
⇒ x²(6x²-5)
And in 12x²-10 we can factor out the GCF (2) to find:
⇒ 2(6x²-5)
And we can use substitution to rewrite the orignal expression as:
⇒ x²(6x²-5)+2(6x²-5)
And in this expression the GCF is 6x²-5 and so after factoring this out we find that:
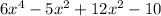 = (x²+2)(6x²-5)
= (x²+2)(6x²-5)