Question

Express (logx a)(loga b) as a single logarithm.

Answer 1

The single logarithm term would be log(b - x)

Step-by-step explanation:

Given:

(logₓ a) (logₐ b)

We have to write it in single logarithm

We have to use the formula

`log_a (m) = (log (m))/(log(a)) \\\\`

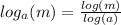
So, we can write (logₐ b) as
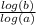`(log (b))/(log(a))` and (logₓ a) as
`(log(a))/(log(x))`

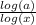
So,

(logₓ a) (logₐ b) =
`(log (a))/(log(x)) X (log (b))/(log (a))`

=
`(log(b))/(log(x))`

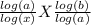
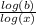
= log (b - x)

Therefore, the single logarithm term would be log(b - x)