Question

On the circuit below, what is the current measured by the ammeter? Each resistor is 50 ohms, and the battery is 50 volts.

A. 0.15 amperes
B. 0.21 amperes
C. 0.27 amperes
D. 0.36 amperes

Answer 1

Answer: C. 0.27 amperes

Explanation:

Gizmos explanation: To find the current in one component of a compound circuit, it is first necessary to find the total resistance and current in the circuit. The ammeter sits on one of two parallel branches. The resistance of the first branch (with the ammeter) is 50 ohms. The resistance of the second branch is 150 ohms. The equivalent resistance of these branches is 37.5 ohms. (1R=150+1150=4150, so R=1504=37.5 ohms.) Adding this to the two 50-ohm resistors in series yields a total resistance of 137.5 ohms. By Ohm's law I=VR, the total current is 50137.5, or 0.36 amps.

Because all of the current must flow through the parallel part of the circuit, the voltage across the parallel elements is equal to the current multiplied by the equivalent resistance, 0.36⋅37.5=13.5 volts. In a parallel circuit, the voltage is the same across each branch, so the voltage across the branch with the ammeter is 13.5 volts. Using Ohm's law again (I=VR), 13.550=0.27 amperes.

Answer 2

C. 0.27 amperes.

Explanation:

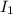`I_1` is the current through the ammeter, and
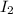`I_2` is the current through the bigger loop.

Going around the circuit loop gives

`V -IR-I_1R-IR =0`

`V -2IR-I_1R =0`

`(1). \: \: V =2IR+I_1R`

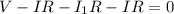
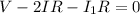
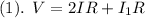
and going around the second loop gives

`V- IR-I_2R-I_2R-I_2R-IR= 0`

`V- 2IR-3I_2R= 0`.

`(2). \: \; V= 2IR+3I_2R`

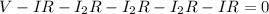
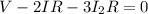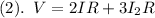
Since

`I = I_1+I_2`,

`I_2 = I-I_1`

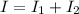putting that into equation (2) we get:

`(3). \: \; V=2IR+3(I-I_1)R= 0`

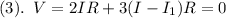
Combining equations (1) and (3) we get:

`2IR+3(I-I_1)R=2IR+I_1R`

`2IR+3IR-3I_1R=2IR+I_1R`

`3IR = 4I_1R`

`\boxed{(4).\: \: I_1 = (3)/(4)I }`

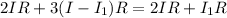
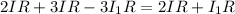
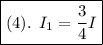
putting this into equation (1) we get:

`V = (11)/(4) IR`

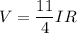
putting in
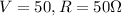`V= 50, R =50\Omega` and we solve for
`I` to get:

`I = (4)/(11) amps`

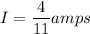
Equation (4) now gives

`I_1 = (3)/(11)amps = 0.27amps`

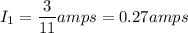
which is the current the ammeter will measure and it is give by choice C.