Question

Water from a leaking tap begins to fall into

an empty tank 0.5 m wide by 2 m long by
4 m high. If the drops fall at a rate of 2 drops
per second, and if each drop weighs 0.05 g,
after how many seconds will the pressure at
the bottom of the tank be 200 Pa?
[Density of water = 1000 kgm and
g= 10 ms ?]​

Answer 1

It will take 20,000 seconds to get a pressure of 200Pa at the bottom of the tank.

Step-by-step explanation:

The pressure at the bottom of the tank will be

`P = (Mg)/(A)`

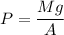
where
`M` is the mass of the water, and
`A` is the base area of the tank.

The base area of the tank is

`A = 0.5m* 2m = 1m^2`,

and if we want the pressure at the bottom to be 200pa, then it must be that

`200Pa = (M(10m/s^2))/(1m^2)`,

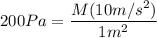solving for
`M` we get:

`M = 20kg\\`

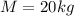
which is the required mass of the water in the tank.

Now, the tank fills at a rate of 2 drops per second or

`2 (0.05g)/s = 0.10g/s = 0.0001kg/s`

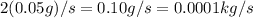
since each drop weights 0.05g.

Therefore, the time
`t` it takes to collect 20kg of water will be

`t = 20kg / (0.0001kg)/(s)`

`t = 2*10^5s`

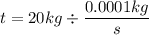
which is 55.56 hours or 2 days and 7.56 hours.

Thus, it will take 20,000 seconds to get a pressure of 200Pa at the bottom of the tank.