Answer:
7x + 3y = 44
Explanation:
The equation of a line in slope- intercept form is
y = mx + c (m is the slope and c the y- intercept )
Rearrange - 3x + 7y = 5 into this form by adding 3x to both sides
7y = 3x + 5 ( divide all terms by 7 )
y =
 x +
x +
 ← in slope- intercept form
← in slope- intercept form
with slope m =

Given a line with slope m then the slope of a line perpendicular to it is
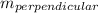 = -
= -
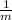 = -
= -
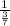 = -
= -
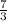 , thus
, thus
y = -
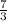 x + c ← is the partial equation
x + c ← is the partial equation
To find c substitute (5, 3) into the partial equation
3 = -
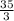 + c ⇒ c = 3 +
+ c ⇒ c = 3 +
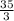 =
=
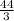
y = -
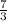 x +
x +
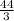 ← in slope- intercept form
← in slope- intercept form
Multiply through by 3
3y = - 7x + 44 ( add 7x to both sides )
7x + 3y = 44 ← in standard form