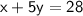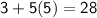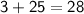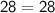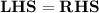Given :-
- Here, We have given two equations that is ,

To Find :-
- We have to find the value of x and y.
Concept used :-
- Linear equations are those equations which having highest power of degree as 1 .
- Linear equations can be solved by subsitute method, elimination method and cross multiplication method.
- Here, I have used substitution method to make calculation easier.
- In subsitute method, you have to subsitute the value of one variable of eq(1) in eq(2) .
Let's Begin :-
Here,
- We have two equations, let consider these two equations as eq(1) and eq(2) that is,
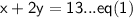
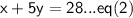
By solving eq(1) :-
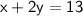
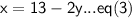
Subsitute eq(3) in eq(2) :-
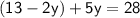
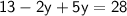
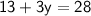
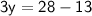
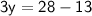
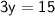
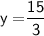
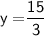
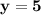
Thus, The value of y is 5
Now,
Subsitute the value of y in eq(1) :-
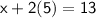
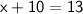
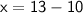
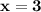
Hence, The value of x and y are 5 and 3 .

Equation 1 :-
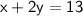
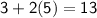
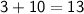
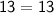
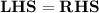
Equation 2 :-