Question

Please someone help!!!!

Kristine observes the top of a lookout tower from a point 220 ft from its base.

If the indicated angle of elevation measures 37º, how tall is the tower? Give your answer to the nearest tenth of a foot.

Answer 1

165.8 ft (nearest tenth)

Explanation:

We can use the tan trig ratio to calculate the height of the tower.

`\sf tan(\theta)=(O)/(A)`

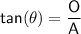
where:

• 
  `\theta` = the angle
• O = the side opposite the angle
• A = the side adjacent the angle

From inspection of the diagram:

• 
  `\theta` = 37°

• O = height of tower (let's call this h)
• A = 220 ft

Substituting these values into the trig tan ratio:

`\sf \implies tan(37)=(h)/(220)`

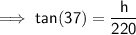
Multiply both sides by 220:

`\sf \implies 220tan(37)=h`

`\sf \implies h=220tan(37)`

`\sf \implies h=165.781891`

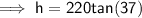
Therefore, the height of the tower is 165.8 ft (nearest tenth)