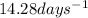Question

Recall that m(t) = (1/2)^t/h for radioactive decay, where h is the half-life. Suppose that a 500g sample of phosphorus-32 decays to 356g over 7 days.

Answer 1

The question is incomplete, here is the complete question:

Recall that m(t) = m.(1/2)^t/h for radioactive decay, where h is the half-life. Suppose that a 500 g sample of phosphorus-32 decays to 356 g over 7 days. Calculate the half life of the sample.

Answer: The half life of the sample of phosphorus-32 is
`14.28days^(-1)`

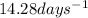
Explanation:

The equation used to calculate the half life of the sample is given as:

`m(t)=m_o(1/2)^(t/h)`

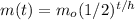
where,

m(t) = amount of sample after time 't' = 356 g

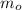`m_o` = initial amount of the sample = 500 g

t = time period = 7 days

h = half life of the sample = ?

Putting values in above equation, we get:

`356=500* ((1)/(2))^(7/h)\\\\h=14.28days^(-1)`

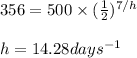
Hence, the half life of the sample of phosphorus-32 is
`14.28days^(-1)`