Answer:
The center is
 .
.
The problem:
What is the center of the circle X2 + y2 = 28+ 3x?
Explanation:
We need to put anything with an
 together and anything with a
together and anything with a
 together:
together:
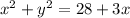
Subtract
 on both sides:
on both sides:
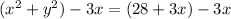
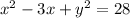
We need to complete the square for
 's. The
's. The
 's are already done.
's are already done.
Keep in mind:
/(2))^2](https://img.qammunity.org/2021/formulas/mathematics/middle-school/xfpgh2kgg5hf8tt33trg4fkx38xb8qamwl.png) on both sides so we can use this identity for the left side with the
on both sides so we can use this identity for the left side with the
 's:
's:
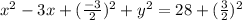
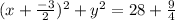
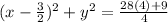
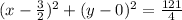
So the center is
 .
.
The radius is
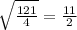 .
.