Answer:
The exact value of x is
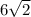
The approximated value of x is 8.49
Explanation:
Let us revise the rules in the right angle triangle when we draw the perpendicular from the right angle to the hypotenuse
In triangle ABC
- Angle B is a right angle
- The hypotenuse is AC
- BD ⊥ AC
1. (AB)² = AD × AC
2. (BC)² = CD × AC
3. (BD)² = AD × CD
4. BD × AC = AB × BC
From the given figure
x represents the length of the ⊥ line from the right angle to the hypotenuse
To find x let us use rule number 3
∵ (BD)² = (AD) × (CD)
∵ BD = x , AD = 3 , CD = 24
∵ x² = 3 × 24
∴ x² = 72
- Use √ for both sides
∴ x =
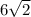
- Find its value by decimal
∴ x = 8.485281374
- Round it to the nearest hundredth
∴ x ≅ 8.49