Please help me I need help please

Question

asked May 5, 2023 210k views

1 Answer

Malthe · Answer 1 · 2023-05-09T22:43:14+0000

Answer:

p = 4

Explanation:

Given equation:

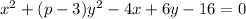
x^2+(p-3)y^2-4x+6y-16=0

Standard equation of a circle:

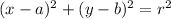
(x-a)^2+(y-b)^2=r^2

(where
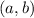(a,b) is the centre of the circle, and
is the radius)

If you expand this equation, you will see that the coefficient of
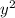y^2 is always one.

Therefore,
p-3=1

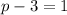
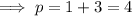
$\implies p=1+3=4$

Additional information

To rewrite the given equation in the standard form:

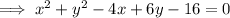
$\implies x^2+y^2-4x+6y-16=0$

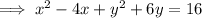
$\implies x^2-4x+y^2+6y=16$

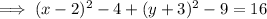
$\implies (x-2)^2-4+(y+3)^2-9=16$

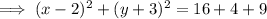
$\implies (x-2)^2+(y+3)^2=16+4+9$

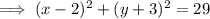
$\implies (x-2)^2+(y+3)^2=29$

So this is a circle with centre (2, -3) and radius √29