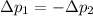Question

During a demolition derby, vehicle 1 collided vehicle 2 going in the opposite direction and came to an immediate stop. If the vehicles are of different masses and were not travelling at the same velocity, what can be concluded about them? *

Answer 1

Their change in momentum is the same in magnitude and opposite in direction

Step-by-step explanation:

The momentum of an object is defined as:

`p=mv`

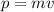
where

m is the mass of the object

v is the velocity of the object

Therefore, the change in momentum of an object is

`\Delta p = m\Delta v`

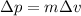
where
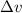`\Delta v` is the change in velocity.

During a collision, the force experienced by an object is equal to the rate of change of momentum:

`F=(\Delta p)/(\Delta t)`

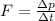
where
`\Delta t` is the duration of the collision.

According to Newton's third law of motion, the force exerted by vehicle 1 on vehicle 2 during the collision is equal (and opposite) to the force exerted by vehicle 2 on vehicle 1, so

`F_1=-F_2`

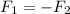
Which means

`(\Delta p_1)/(\Delta t)=-(\Delta p_2)/(\Delta t)`

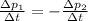
And since the duration of the collision is the same for the two vehicles, this becomes

`\Delta p_1 =-\Delta p_2`