Question

Let the region R be the area enclosed by the function f(x)=ln(x) and g(x)= 1/2x-2. Find the volume of the solid generated when the region R is revolved about the line y=-5.

Answer 1

`V=61.66`

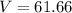
Explanation:

This problem can be solved by using the expression for the Volume of a solid with the washer method

`V=\pi \int \limit_a^b[R(x)^2-r(x)^2]dx`

where R and r are the functions f and g respectively (f for the upper bound of the region and r for the lower bound).

Before we have to compute the limits of the integral. We can do that by taking f=g, that is

`f(x)=g(x)\\ln(x)=(1)/(2)x-2`

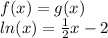
there are two point of intersection (that have been calculated with a software program as Wolfram alpha, because there is no way to solve analiticaly)

x1=0.14

x2=8.21

and because the revolution is around y=-5 we have

`R=ln(x)-(-5)\\r=(1)/(2)x-2-(-5)\\`

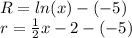
and by replacing in the integral we have

`V=\pi \int \limit_(x1)^(x2)[(lnx+5)^2-((1)/(2)x+3)^2]dx\\`

`V=\pi [28x+(1)/(x)+xln^2x-12xlnx-6lnx]`

and by evaluating in the limits we have

`V=61.66`

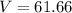
Hope this helps

regards