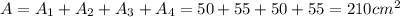Question

The LATERAL Surface Area for the shape below is ____________. (assume the bases are the larger faces on the top and bottom.)

Answer 1

`210 cm^2`

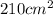
Explanation:

In this problem, we want to find the lateral surface area of the prism.

Since the bases are the larger faces on top and on bottom, we have to exclude those faces from the calculation.

So, the lateral surface area is just the sum of the areas of the other 4 faces.

We have:

- Face 1: 5 cm x 10 cm

Area:
`A_1 = 5\cdot 10 = 50 cm^2`

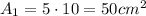
- Face 2: 5 cm x 11 cm

Area:
`A_2 = 5\cdot 11 = 55 cm^2`

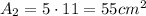
- Face 3: 5 cm x 10 cm

Area:
`A_3 = 5 \cdot 10 = 50 cm^2`

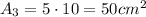
- Face 4: 5 cm x 11 cm

Area:
`A_4 = 5\cdot 11 = 55 cm^2`

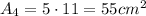
Therefore, the total lateral surface area is:

`A=A_1+A_2+A_3+A_4=50+55+50+55=210 cm^2`