Answer:
Because the opposite side is shorter than the hypothenuse
Explanation:
- An acute angle is an angle which is less than
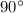
- A right angle is an angle equal to
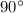
- An obtuse angle is an angle which is between
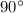 and
and
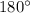
In a right triangle, we have 1 right angle and 2 acute angles.
The sine of an angle in a right triangle is defined as:
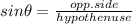 (1)
(1)
where
At the numerator we have the length of the side opposite to the angle
At the denominator we have the length of the hypothenuse
In a right triangle, the hypothenuse is the longest side of the triangle, so we have
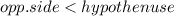
Therefore, the ratio in the eq(1) is less than 1, therefore, the sine of the angle is less than 1. Also, the sine is positive, since the ratio in the equation is a positive number.