What are the zeros of the function below? F(x)= (x-1)(x+1)/6(x-4)(x+7)

Question

asked Sep 28, 2021 96.6k views

1 Answer

Sven Liebig · Answer 1 · 2021-10-03T17:43:09+0000

Answer:

+1 and -1

Explanation:

The function in this problem is:

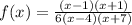
f(x)=((x-1)(x+1))/(6(x-4)(x+7))

First of all, we have to define the domain of the function, which is the set of values of x for which the function is defined.

In order to find the domain, we have to require that the denominator is different from zero, so

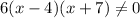
$6(x-4)(x+7)\\eq 0$

which means:

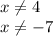
$x\\eq 4\\x\\eq -7$

So the domain is all values of x, except from 4 and -7.

Now we can solve the problem and find the zeros of the function. The zeros can be found by requiring that the numerator is equal to zero, so:

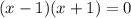
(x-1)(x+1)=0

This is verified if either one of the two factors is equal to zero, therefore:

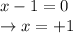
$x-1=0\\\rightarrow x=+1$

and

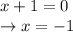
$x+1 = 0\\\rightarrow x=-1$

We see that both values are part of the domain, so they are acceptable values: so the zeros of the function are +1 and -1.