Answer:
speed of the current is 6 miles per hour.
Speed of the boat in still water is 18 miles per hour
Explanation:
-Speed is defined as displacement over time.
-Let a be the speed in still water and b be speed of the current of the river.
#The speed downstream is equated as:
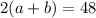
#The speed upstream in 4hrs is equated as:
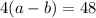
we make a the subject of the formula in i and substitute in ii:
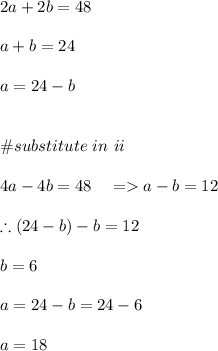
Hence, speed of the current is 6 miles per hour and
Speed of the boat in still water is 18 miles per hour