Question

A car is strapped to a rocket (combined mass = 661 kg), and its kinetic energy is 66,120 J.

At this time, the rocket runs out of fuel and turns off, and the car deploys a parachute to slow down, and the parachute performs 36,733 J of work on the car.

What is the final speed of the car after this work is performed?

Answer 1

9.43 m/s

Step-by-step explanation:

From law of conservation of energy, the initial magnitude and final magnitude of work is same. The magnitude of work done by car finally is given by getting the differences between the initial kinetic energy and work done by parachute on car hence 66120-36733=29387 J

Kinetic energy,
`KE=0.5mv^(2)`

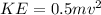
Making v the subject of the formula then

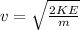`v=\sqrt {(2KE)/(m)}` where m is the mass and v is the velocity of the car.

Substituting 29387 J for Ke and 661 Kg for mass then

`v=\sqrt {(2* 29387)/(661)}=9.42957 m/s\approx 9.43 m/s`