Question

A phone company offers two monthly plans. Plan A costs $19 plus an additional $0.11 for each minute of calls. Plan B costs $10 plus an additional $0.13 for each minute of calls. For what amount of calling do the two plans cost the same? minutes What is the cost when the two plans cost the same? $

Answer 1

Part 1) When the amount of calling is 450 minutes the two plans cost the same

Part 2) When the two plans cost the same , the cost is $68.50

Explanation:

Part 1) For what amount of calling do the two plans cost the same?

Let

x ---> the number of minutes

y ----> the total cost

we know that

The linear equation in slope intercept form is equal to

`y=mx+b`

where

m is the slope or unit rate of the linear equation

b is the y-intercept or initial value

In this problem we have

Plan A

The slope is equal to

`m=\$0.11\ per\ minute`

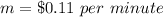
The y-intercept is

`b=\$19`

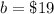
substitute

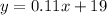`y=0.11x+19` ----> equation A

Plan B

The slope is equal to

`m=\$0.13\ per\ minute`

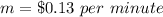
The y-intercept is

`b=\$10`

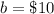
substitute

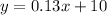`y=0.13x+10` ----> equation B

Equate equation A and equation B

`0.13x+10=0.11x+19`

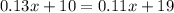
solve for x

`0.13x-0.11x=19-10\\0.02x=9\\x=450`

therefore

When the amount of calling is 450 minutes the two plans cost the same

Part 2) What is the cost when the two plans cost the same?

substitute the value of x=450 minutes in equation A or equation B and solve for y

`y=0.11(450)+19=68.5`

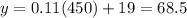
therefore

When the two plans cost the same , the cost is $68.50