Question

a flat roof 22 feet long and 12 feet wide has an 8 inch depth of water sitting on it. What is the weight of the water on the roof?

Answer 1

see the explanation

Explanation:

step 1

Find the volume of the water

we know that

The volume of water on the roof can be found by multiplying the length of the roof by the width of the roof by the depth of the water.

so

`V=LWH`

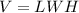
where

L is the length

W is the width

H is the deep of the water

Remember that

`1\ ft=12\ in`

we have

`L=22\ ft\\W=12\ ft\\H=8\ in=8/12=2/3\ ft`

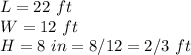
substitute

`V=(22)(12)(2/3)=176\ ft^3`

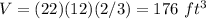
step 2

Find the weight of the water

we know that

The density of water is equal to

`62.4\ (lb)/(ft^3)`

Multiply the density by the volume to obtain the weight of the water

`62.4(176)=10,982.4\ lb`

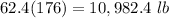
Convert to kilograms

Remember that

`1\ lb=0.45\ kg`

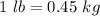
so

`10,982.4\ lb=10,982.4(0.45)=4,942.08\ kg`

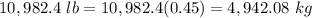
That's 4.9 tons of water pushing down on that roof