Question

=

15. Given a rectangle ABCD with AD 12. The diagonals AC and BD intersect at point O such that
mZDOC = 30°. Find the area of the rectangle.

Answer 1

To find the area, we need to find the side length AB (and DC).

The easiest way to approach this is to draw a sketch with all the given information (see attached).

As point O is the center point of the rectangle, we can draw a horizontal line from point O to the center point of BC (point M on the diagram) and create a right triangle. We can then use the Sine rule to find the shortest leg of the triangle (marked as x on the diagram). This will be half of the side length AB, and so to find the side length, simply multiply it by 2.

To find the missing angles of the right triangle:

m∠COM = (180° - 30°) ÷ 2 = 75°

m∠OCM = 180° - 90° - m∠COM = 90° - 75° = 15°

Sine rule

`\sf (a)/(sinA)=(b)/(sinB)=(c)/(sinB)`

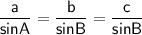
(where A, B and C are the angles and a, b and c are the sides opposite the angles)

`\implies (x)/(\sin(15))=(6)/(\sin(75))`

`\implies x=\sin(15)\cdot (6)/(\sin(75))`

`\implies x=12-6√(3)`

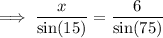
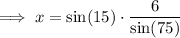
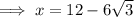
As AB =
`2x`

`\begin{aligned} \implies AB & =2x\\ & =2(12-6√(3))\\ & =24-12√(3)\end{aligned}`

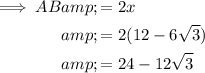
Now we have both side lengths of the rectangle, we can easily calculate the area.

Area of a rectangle = width × length

= (24 - 12√3) × 12

= 288 - 144√3

= 38.5846837...

= 38.585 units² (nearest thousandth)