Question

What is the sum of the first 30 terms of the arithmetic sequence : -3,0,3,6...84

Answer 1

`1,215`

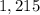
Explanation:

we have

`-3,0,3,6...84`

`a_1=-3\\a_2=0\\a_3=3\\a_4=6`

`a_2-a_1=0-(-3)=3`

`a_3-a_2=3-0=3`

`a_4-a_3=6-3=3`

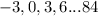
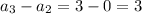
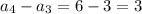
so

The common difference d is 3

we know that

The rule to find the sum of the the first n terms of the arithmetic sequence is equal to

`S=(n)/(2) [2a_1+(n-1)d]`

where

d is the common difference

a_1 is the first term

we have

`d=3\\a_1=-3\\n=30`

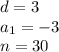
substitute in the formula

`S=(30)/(2) [2(-3)+(30-1)3]`

`S=15[-6+87]`

`S=1,215`