Question

H(x)=1/8x^3-x^2 what is the average rate of change of h over the interval -2

Answer 1

the average rate of change of h is 1/2 .

Explanation:

Here we have , a function h(x)=1/8x^3-x^2 or ,
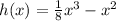`h(x)=(1)/(8)x^3-x^2` . We need to find rate of change of function over
`-2<x<2` . Let's find out:

We know that , Rate of change of function is :

`(f(b)-f(a))/(b-a)`

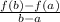
According to question we have ,

⇒
`(f(-2)-f(2))/(-2-2)`

`f(-2) = (1)/(8)(-2)^3-(-2)^2 = (1)/(8)(-8)-4 = -5\\f(2) = (1)/(8)(2)^3-(2)^2 = (1)/(8)(8)-4 = -3`

⇒
`(-5-(-3))/(-2-2)`

⇒
`(-2)/(-4)`

⇒
`(1)/(2)`

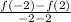
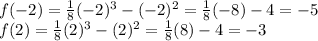
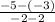
Therefore , the average rate of change of h is 1/2 .