Question

An eastbound train left at 12pm. Four hours later, a westbound train left the same station. At 8pm, the two trains were 400 miles apart. Find the rate of each train if the westbound train traveled 10 miles per hour faster than the eastbound train.

Answer 1

Explanation:

E + W = 4

95E + 110W = 400

E = Eastbound time; W = Westbound time

E + W = 4 → total time

d = rt

Eastbound distance 95E; Westbound distance → 110W

Total distance → 95E + 110W = 400

Answer 2

Explanation:

Gotta love these motion problems!

d = rt is what we need here to solve this, along with some logic.

If the EB (eastbound) train left at noon then at the end of its travels, at 8pm to be specific, it was traveling for 8 hours. Therefore, for the EB train, t = 8.

If the WB train left at 4 pm then at the end of its travels, also at 8pm, it was traveling for 4 hours. Therefore, for the WB train, t = 4.

The distance between the trains is given as 400 miles. That 400 mile distance is due to the fact that each train traveled a distance of rate*time. The distance the WB train traveled + the distance the EB train traveled = 400 miles. Now we just need to find out the distance each traveled in its respective time frame.

For the EB train. We already know that t = 8. We do not know how fast it's going, so rate is just r. In the distance formula, d = rt:

`d_(EB)=8r`

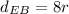
For the WB train. We already know that t = 4. We do not know this rate either, but we do know that it is traveling 10 mph faster than the EB train, so rate is r + 10. In the distance formula, d = rt:

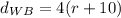`d_(WB)=4(r+10)` and

`d_(WB)=4r+40`

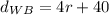
We have already determined that

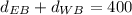`d_(EB)+d_(WB)=400` so

4r + 40 + 8r = 400 and

12r + 40 = 400 and

12r = 360 so

r = 30

That means that the EB train is traveling 30 mph and the WB train then has to be traveling 40 mph.

These are quite difficult...I get it. They drive all my students, regardless of what math level they are in, absolutely batty!!!