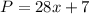Answer:
The equation which can be used to find p, the perimeter of the heptagon will be:
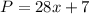
Explanation:
As
- The length of each of the sides of a heptagon are
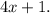
let 's' be the the length of one of the seven congruent sides of a regular heptagon.
so
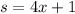
- As all sides of a regular heptagon have the same length.
so
The perimeter P, can be by using the following formula:
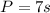
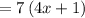


Therefore, the equation which can be used to find p, the perimeter of the heptagon will be: