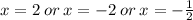Question

Use synthetic division to show that the number given to the right of the equation is a solution of the equation. Then solve the polynomial equation.

2x^(3)+x^(2)-8x-4=0; 2

Answer 1

`x = 2 \: or \: x = - 2 \: or \: x = - (1)/(2)`

Explanation:

The given polynomial equation is

`2 {x}^(3) + {x}^(2) - 8x - 4 = 0`

We perform the synthetic division as shown in the attachment by dividing by x-2.

This gives a remainder of 0 and a quotient of

`2 {x}^(2) + 5x + 2`

This means the polynomial equation becomes:

`(x - 2)(2 {x}^(2) + 5x + 2) = 0`

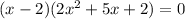
We factor the quadratic term by splitting the middle term;

`(x - 2)(2 {x}^(2) + 4x +x + 2) = 0`

`(x - 2)(2 x(x+ 2) +1(x + 2) )= 0`

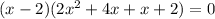
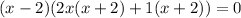
Collect common factors again:

`(x - 2)((x+ 2)(2x + 1) = 0`

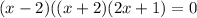
The solution is:

`x = 2 \: or \: x = - 2 \: or \: x = - (1)/(2)`